- concavo nel caso del "triangolo" grande in alto e
- convesso in quello in basso (dove l'area della parte in esubero equivale a quella del fantomatico quadratino che rimane appunto vuoto).
- «Con un trucco simile un falsario americano tagliava le banconote da 100 dollari, facendo saltare fuori una tredicesima banconota ogni 12 tagliate. ho della documentazione da qualche parte.... su un "Enigmi e Giochi Matematici" di Martin Gardner. Cerca anche un puzzle chiamato "Uscita dal Mondo" di H.S.M Coexter, se non mi sbaglio (non so il nome originale). bello, molto bello comunque.» (Aaron)
- «Hai altri aneddoti simili? tipo dimostrare l'ultimo teorema di Fermat: Non esiste una terna di numeri INTERI positivi A,B,C tali che An + Bn = Cn (con n>2) Se ce la fai entro il 13 settembre 2007 puoi presentarti all'Università di Göttingen dove ci sono in palio 50.000 Euro (100.000 marchi nel bando del 1908). Ne so un altro di aneddoto: Sai perchè ai matematici non danno il premio nobel? Perchè Riemann (quello del calcolo integrale) si faceva la moglie di Nobel ed è stato scoperto...hehehe così adesso i matematici si accontentano della medaglia Filtz...» (Pandos)
Vedi anche: Controllo-della-Mente Jedi, L'emisfero sinistro è un gran rompipalle e Test: quanto sei intelligente?

|

|

TI RIMANGONO APPENA PER LEGGERE "IL LIBRO"
Questa pagina è stata visitata 8424 volte dal 17 Giugno 2004.
Dimensione: 5475 bytes Ultimo aggiornamento: lunedì 3 maggio 2010 h.19:38
(Per non mostrare più l'intestazione delle pagine, clicca qui.)
 Il triangolo impossibile - soluzione
Il triangolo impossibile - soluzione
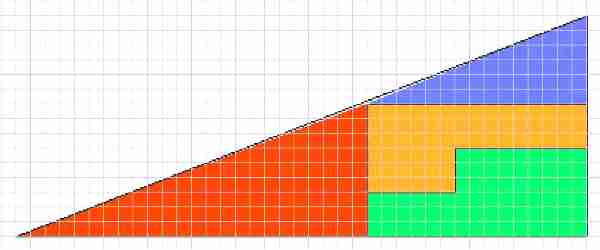
I due triangoli non sono uguali.
Anzi, a ben vedere, non si tratta neppure di triangoli, bensì di quadrilateri: disegnandoli con precisione, noteremo che dove il triangolino blu si unisce al triangolino rosso si origina un "dosso":
Disegnandoli correttamente, quelli che sembrano triangolini di 2x5 e 8x3 risultano leggermente più grandi o più piccoli: ad es. nel triangolino blu, se l'altezza resta fissa a 2 la base risulta 5,2 - mentre se la base resta fissa a 5 l'altezza risulta circa 1,9 (Paolo)
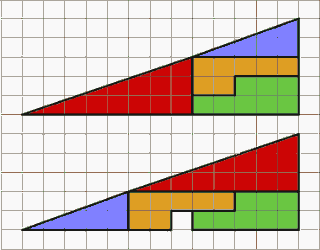 Matematicamente parlando, osserviamo che i due triangolini blu e rosso sembrano triangoli simili (cioè con tutti e tre gli angoli uguali) ma non lo sono: infatti, confrontandone l'inclinazione delle ipotenuse, si ottiene rispettivamente 2/5 = 0,4 e 3/8 = 0,375 (CE).
Matematicamente parlando, osserviamo che i due triangolini blu e rosso sembrano triangoli simili (cioè con tutti e tre gli angoli uguali) ma non lo sono: infatti, confrontandone l'inclinazione delle ipotenuse, si ottiene rispettivamente 2/5 = 0,4 e 3/8 = 0,375 (CE).
 Se invece i triangolini fossero triangoli simili, allora il rosso risulterebbe di una fettina più corto (vedi figura qua accanto) - e l'area di questa fettina corrisponde appunto al quadratino in esubero. (Nicolò)
Se invece i triangolini fossero triangoli simili, allora il rosso risulterebbe di una fettina più corto (vedi figura qua accanto) - e l'area di questa fettina corrisponde appunto al quadratino in esubero. (Nicolò)
 Ma, ricomponendo i pezzi, si otterrebbe quest'altro quadrilatero. (Che appunto sembra un triangolo, ma a ben vedere la presunta ipotenusa è "spezzata" nel punto in cui il triangolo blu si congiunge al pezzo giallo.)
Ma, ricomponendo i pezzi, si otterrebbe quest'altro quadrilatero. (Che appunto sembra un triangolo, ma a ben vedere la presunta ipotenusa è "spezzata" nel punto in cui il triangolo blu si congiunge al pezzo giallo.)

CURIOSITÀ